
The following question was recently sent to me: suppose a firm uses a blended benchmark that rebalances quarterly… how should they calculate external dispersion? I guess I hadn’t given much thought to the possible challenges with rebalancing quarterly benchmarks, but a solution came to me rather quickly, that I want to share with you. Of course, feel free to “chime in,” should you have other thoughts or find some flaw in my logic.
Rebalancing 101: when to?
Before we talk about how to rebalance a quarterly blended benchmark, let’s briefly discuss the “when to” do it.
In my view, the timing for rebalancing a benchmark should coincide with the timing to rebalance the portfolio. The benchmark is to align with the benchmark’s strategy, yes? And so, one way to do this is to ensure the rebalancing timing aligns.
How to go about rebalancing quarterly benchmarks
Let’s say that your benchmark allocation consists of 60% S&P 500 and 40% Bloomberg Barclays’ Agg. You’ve elected to rebalance quarterly. Recall that the Global Investment Performance Standards (GIPS®) requires you to provide a 36-month, ex post, annualized standard deviation (what is referred to in the question as “external dispersion,” a term I’ve learned to dislike). If you rebalanced monthly, this wouldn’t be a challenge. But since you’re rebalancing quarterly, how do you come up with the appropriate blended benchmarks for the other two (non-rebalanced) months?
We’ll use the following information to walk through the approach I came up with: 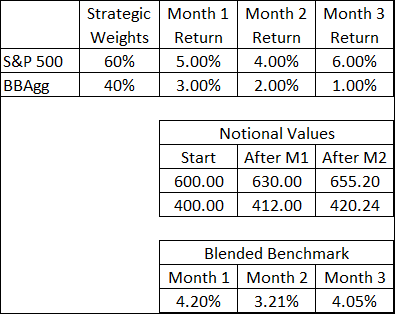
We see in the top panel the returns for the two indexes for the three months, as well as our target allocation: 60/40. I’m using notional values to allow us to capture the changes to the benchmark for the second and third months, where rebalancing isn’t occurring.
Month 1: Standard rebalancing logic
Month 1 is the month we rebalance, so our Blended Benchmark for the month is simply:
where:
i represents the different individual indexes
A = the strategic allocation for index i
r = benchmark return for index i
This is pretty standard practice, yes?
Month 2: Adjusting the blended benchmark to reflect prior period results
Okay, so now we move to the tricky part: how to blend the second and third months’ benchmark returns without rebalancing? This is where the notional values come in. As can be surmised, we start with $1,000 (or £, €, whatever). We first adjust these values for the effect of the returns from the first month. This is simply:
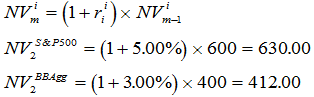
where:
NV = notional [dollar] value
m = the individual month we’re working on; in this case, it’s the second month
These amounts reflect how each benchmark changed, but using notional values. And these are what we will use to derive our blended benchmark for the second month:
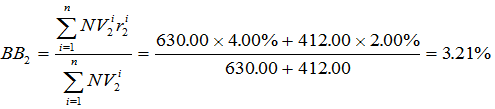
If you follow this same logic for Month 3, you will get the result (4.05%) that appears above.
Simple, intuitive, logical approach to rebalancing quarterly benchmarks
I think this is a rather intuitive approach; well, it’s intuitive to me. And, fairly simple (Too simple? Am I missing something?)
What do you think about it? Do you have other ideas, have any issues with my approach, see flaws? Please feel free to send in your comments or questions; thanks!
Oh, and I’ll have a bit more to say on this in the August newsletter. Plus, I’ve decided to incorporate this into our Fundamentals of Investment Performance Measurement class! I’ll be teaching an in-house class shortly for one of our clients!
