Linking monthly standard deviation has its root within the AIMR-PPS
One advantage to being a bit older than most folks in performance measurement is that I have been exposed to a lot of ideas, and quite a bit of history. This includes the predecessor standard to GIPS®) the AIMR Performance Presentation Standards or AIMR-PPS®.
Some very quick background. AIMR was the Association for Investment Management & Research. It was created in 1990, when the Financial Analysts Federation merged with the Institute of Chartered Financial Analysts. Several years ago AIMR became the CFA Institute.
The AIMR-PPS went into effect in January 1993. The prior year, as things were being finalized, the AIMR-PPS Implementation Committee issued a paper that explained how to link monthly composite standard deviations to arrive at an annual value. They then issued an errata that corrected the earlier formula.
But, the AIMR-PPS standard deviation linking formula disappeared!
The AIMR-PPS Implementation Committee did not include this formula with the Standards. I called Sue Martin, CFA , (or it may have been Cindy Kent; please excuse my “senior moment”) to find out why. Sue oversaw the AIMR-PPS at the time, and Cindy worked with Sue. Sue (or Cindy) told me they learned that the idea of linking standard deviations is flawed. She also sent me a paper that explained why. I probably have the original formulas as well as the paper somewhere in my files; suffice it to say: we were told to forget about the idea of linking monthlies to obtain annuals. And so, I put the idea behind me.
Fast forward: a recent GIPS verification
I recently conducted a GIPS verification for a new client. It was their first, since they’ve only recently become compliant.
In the course of my review, I asked to see how they arrived at the composite’s dispersion. They provided me with a spreadsheet, and pretty quickly I determined that they were trying to bring monthly standard deviation values together to arrive at an annual. They apparently wanted to somehow average the monthlies. They had used a consultant to do this work for them, and this consultant had familiarity with their portfolio accounting system. The consultant thought that this idea seemed logical.
Well, my initial reaction was “you can’t do this.” But then I thought that perhaps he had discovered a method that could work, so why not be open to it? But after a quick test I found that their result wasn’t close to the actual. I then pondered the idea a bit.
But why doesn’t it work? Why can’t we link monthly standard deviations?

I recall that the paper that I was given from AIMR provided a fairly technical reason as to why it’s not possible to link monthly standard deviations. But, it doesn’t have to be difficult to understand why.
Consider the following composite:
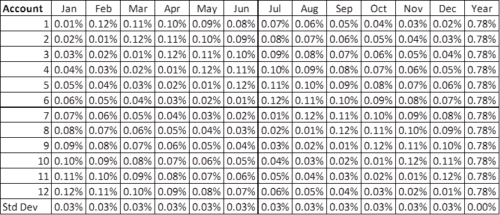
We see that each account experiences the same result as every other account. They range from 0.01% to 0.12%, or 1 basis point to 12 basis points. We also see that no two accounts have the same return for any given month, and no account has the same return in more than one month.
Pretty simple, right?
And so, for each month we get the same standard deviation (0.03%). Since each account experiences the same 12 monthly returns (just not in the same order), they all get the same annual return (0.78%), and dispersion is 0.00 percent.
Now, let’s look at a second composite:
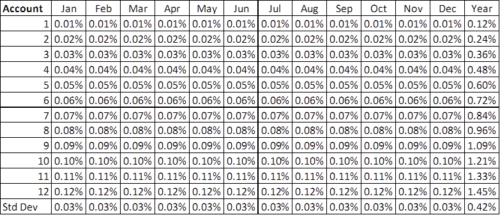
In this scenario, each account has the same return for each month, ranging from 0.01% to 0.12 percent. Again, no two accounts have the same return for any month. As a result, they all have different annual returns, ranging from 0.12% to 1.45 percent.
Because the individual accounts have the same experience each month, the standard deviations remain the same for the full year (0.03%). But because the annual returns differ, the annual standard deviation is much higher than we saw in the first example.
Now, let’s consider both composites
Okay, so what’s actually going on here?
For each composite, every month has the exact same standard deviation. This means that whatever method you use to link, combine, or average them, you should end up with the same “annual” value. However, we can also see that in reality the annual standard deviations differ. This means that annual standard deviation has no relationship to monthly, further meaning that to try to link is a waste of time.
Who else is doing this (“linking, averaging, combining” monthly standard deviation)?
This is a topic that I have not dealt with in almost 25 years. So imagine my surprise when I saw that someone had implemented it. If one firm has, perhaps others have, too?
For the most part, I think this falls into the “academic” category. That is, it’s kind of interesting, but nothing we really need to be concerned with. However, if there are firms that are doing this, regardless how, guess what: it doesn’t work!
Or, am I missing something? If you think I am, please chime in!
